In the video "Crop Circles - The Research" it is shown that different elements within a crop circle are in size and placing far from random. These elements follow strict geometrical rules. The rules of geometrical constructions. For those who haven't seen this video I will briefly repeat what is being discussed in the documentary.
Let's have a look at the formation that appeared at Winterbourne Basset in 1996, the so-called 'Harlequin'. It is easy to reconstruct this formation. After a few reconstruc-tion steps we get the situation as shown in the first diagram. Notice that nothing in the diagram is random. Every element is determined by previous elements. Now the central circle is reconstructed again, but now in a different place. Look at the second diagram to see where this place is and notice that previous steps also determine this spot! Diagram three is the result.
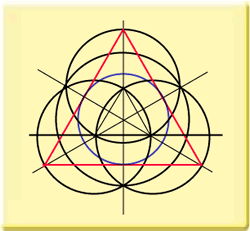
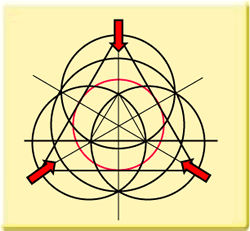
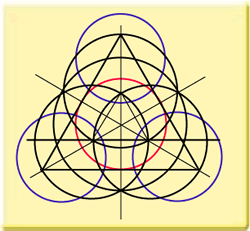
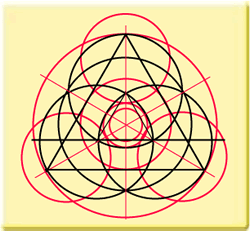

What can be learned from the reconstruction of the 1996 Winterbourne Basset formation? First of all, like I envisaged already, we could see that the different elements in the final design are in size and placing all determined by previous steps, determined by strict geometrical rules. Secondly, and this is at least of equal importance, we can see that several constructed elements can no longer be found when we reach the final design. These elements were strictly necessary for the ensuing steps but were then 'rubbed out'. A good example is the large circle that was necessary to determine the placing of the three outer circles. This large circle cannot be found in the final stage of the design! This is something that can be accomplished easily on paper, but is impossible to perform in standing crop. You cannot make downed crop stand again! I also ask you to notice that since the big triangle determines the size of the three outer circles, it is obvious that these three circles have a special ratio to the overall circle. A diatonic ratio. In this case an octave. This is not something special or coincidental. It is an element of the logic of geometry.
The formation at Winterbourne Basset was not the only one to show how strict geometrical rules
were followed by the different elements in the formation. The 'Crescents' formation of 1999 at
Barbury Castle showed the same features. The following diagrams show which rules were followed
by the crescents and why there is a diatonic ratio within the crescents. The ratio is 9/4,
which is the note D in the second octave.
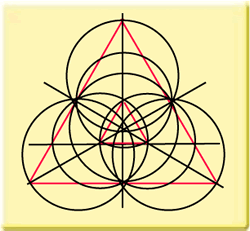
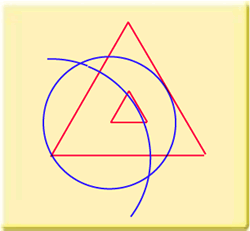
The first diagram shows the situation after a few construction steps. The smaller triangle and the larger triangle form once more a diatonic ratio. In this case 16, which is the 5th octave. Let me emphasize again that this is not a coincidence. It is the logical result of the geometrical construction. The next step is very important. Construct a circle with its centre in the left corner of the large triangle and with it's perimeter just touching the side of the small triangle. Now do the reverse! Construct a circle with its centre in the left corner of the small triangle and with it's perimeter just touching the large triangle. The two circles overlap and form a crescent. This crescent is exactly at the same place and of the same size and shape as could be found in the Barbury Castle formation of 1999. Because of the way it is constructed, because of the way it follows those strict geometrical rules, it is logical that the crescent has a diatonic ratio in it. The ratio is 9/4. The note D in the second octave.
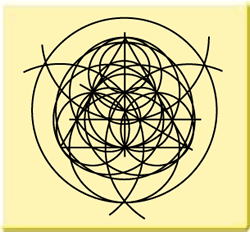

Here again we see that necessary elements in its construction, cannot be found back in the final design. The two triangles were absolutely necessary to construct the crescents, but the triangles don't show up in the final design. They disappeared, were rubbed out. You can do that on paper, but not in crop!
When you study more crop circles you will find that this goes for a lot of formations. Three conclusions can be drawn:
The size and placing of the different elements in a crop formation are not random but do follow
strict geometrical construction rules.
Because of the internal geometry some elements will have special (diatonic) ratios to other elements. Some absolutely necessary for the construction elements of the design cannot be found in the final formation.
For more information on crop circle geometry
click here or get hold of the booklet "Crop Circle Reconstructions and Geometry".
© Bert Janssen 2000.