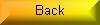
And here as well we find the necessary construction points exactly on the edge of the standing crop.

If the inner circle of the standing crop had been just a tiny bit bigger, this formation
could not have been constructed without damaging the standing crop. But also this formation
has the perfect size. Coincidence?
The formation of Etchilhampton of 1997 leads us even further.
Via many steps we are able to reconstruct the final pattern, which shows the following
construction points:
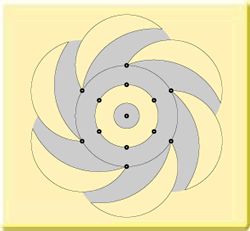
In order to construct this formation, we need several points that lie relatively far from
the centre. This could have been a problem, but the ring around the formation brought help.
Coincidence?
Inside the formation the outer construction point also lies just in the flattened crop.
Coincidence?
Does this mean that we should only be focusing on the construction points?
No. These points are merely one of many indicators that show us that the crop circle
formations are formed via an extremely precise geometric pattern. The are made with
geometric principles that are so well known to us.
What can we do with this knowledge? What does it tell us? One of the things is that, since
they are all created from the same basic pattern, we can compare them with each other. For
instance, we can compare their size, thanks to the basic pattern which enabled us to
superimpose the various formations. Moreover, now that we know their internal geometry,
we can make them three-dimensional. And as we saw before in the basic pattern, every crop
circle formation is based on a equilateral triangle, which is a tetrahedron
three-dimensionally. By means of the above mentioned geometry, the pictograms can be
turned into three-dimensional figures based on mere tetrahedrons!
Every single element inside a formation is related by definition to all other elements
inside that formation because of this geometry. Diatonic ratios are a logic result of this.
But it goes even further. Every single element of a formation can be related to ever single
element of another formation!
So far, we have only looked at sixfold geometry. But what about fivefold geometry that we
find, for instance, in the Star of Bethlehem from 1997?
By means of the basic pattern this is how we can come to fivefold geometry:
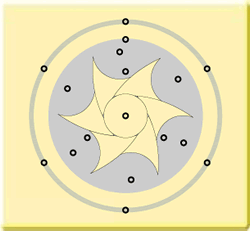
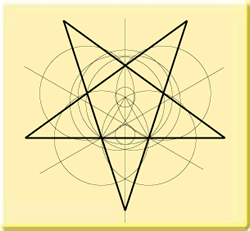
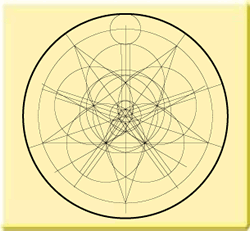
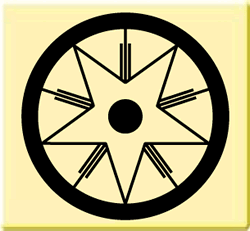
If the inner circle were one inch smaller, we would have had a problem. Coincidence?
What you just saw is only the surface of the fascinating world of the crop circles' inner
geometry. What I found out goes a lot further than described on these pages. For instance, it
can be proved that Avebury's Web is an amalgamation between five- and sixfold geometry. Both
geometries are interlocking in this extraordinary formation. Perhaps this perfect geometry is
not telling us anything. Perhaps it is just needed to make the pictograms beautifully harmonic,
which has a hypnotising effect on people. Perhaps the fact that the construction points are
never in the standing crop is done on purpose to show us we're on the right track with this
form of geometric analysis.
© Bert Janssen 1997.
For questions or information,
e-mail Bert Janssen.