What is it that makes crop circles such a fascinating phenomenon? No doubt the mysterious
and inexplicable aspect plays a mayor role here, but is that all? How can it be explained
that people get so fascinated merely by looking at them? Even when they don't know a single
thing about the crop formations, the symbols seem to stir up interest nevertheless.
The question why this is has kept me occupied for many years now. There's something about
the pictogrammes that has some kind of hypnotising effect on people. But why?
From the very first crop circle formations, people like John Martineau and Wolgang Schindler
have worked with geometry. They mostly aimed at the 'outside' of the pictogrammes. Until 1992
many formations indeed could be fit into fivefold geometry. But in 1992 the formations
changed, and their geometrical explanations no longer held. Later Gerald Hawkins intensively
studied the various elements within the crop circles. He found strong indications for the
existence of diatonic ratios in the patterns. Although all these results are indeed
fascinating, they weren't enough for me, to be honest. There had to be more. A more
fundamental basis. And I found it. Many crop circles are built on simple but enlightening
geometry. Geometry that provides us with certain results, certain derivatives, such as the
findings of Martineau, Schindler and Hawkins. Geometry that is the basis, the source, the
cause of their findings. The internal geometry of crop circles.
It all started with my attempts to reconstruct certain formations on paper by means of a ruler
and a pair of compasses. I didn't use the ruler to measure, only to draw straight lines. I was
therefore working with mere construction. The results were fascinating:
1.All formations I studied turned out to have exactly the same basic pattern.
2.All elements in a formation (and, as a result, all internal proportions as well) are
not coincidental, but strict results from their construction.
3.The necessary construction points (centres of used circles) can never be found in
standing crop.
This is how it works.
The above-mentioned basic pattern looks like this:
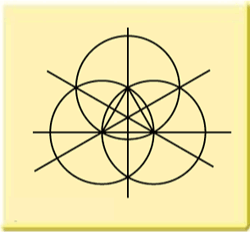
From this basic pattern many formations can be constructed. Let's now try to reconstruct a
formation, a relatively simple one. Let's try the Harlequin formation of 1997.
Via several simple construction steps we come to this diagram:
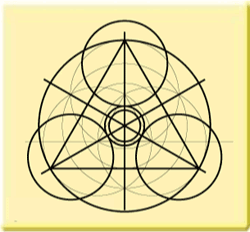
This diagram shows an equilateral triangle, constructed in the three circles necessary to
make the basic pattern and is the same as we can see in the Harlequin formation. Please
notice the circle constructed neatly in the triangle. It's the same circle as those three
constructed on the corners. Coincidence?
The inner circle in the formation fits exactly in the equilateral triangle of the basic pattern.
Coincidence?
The end result looks like this:

I must admit that this is a relatively simple and obvious formation. The next formation however shows us differently. Starting off with the same basic pattern we can reconstruct the following through mere 15 steps:
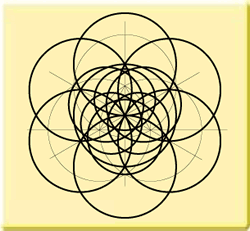
It seems a variety of lines and circles, but in reality it is the internal geometry of the following pictogram:

In spite of the complex character of this formation, it can be constructed without trampling the standing crop. The following diagram shows the position of the necessary construction points. As you can see they all lie in the flattened crop.
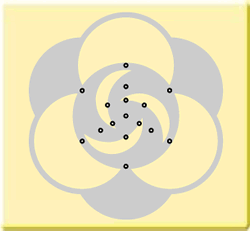
Some construction points lie exactly on the edge of the standing crop. It all fits just
perfectly. If, for instance, the central circle had been just a little bit smaller, the
formation could not have been made without damaging the standing crop. 'Luckily', the
central circle has the perfect shape. Coincidence?
We see the same principle when looking at the following formation. Starting off from the
basic pattern we reconstruct through.

